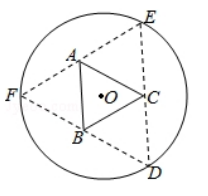
16. (5 分) 如图, 圆形纸片的圆心为 O, 半径为 $5 \mathrm{~cm}$, 该纸片上的等边三角形 $A B C$ 的中心为 $O . D 、 E 、 F$ 为圆 $O$ 上的点, $\triangle D B C, \triangle E C A, \triangle F A B$ 分别是以 $B C$ , $C A, A B$ 为底边的等腰三角形. 沿虚线前开后, 分别以 $B C, C A, A B$ 为折痕 折起 $\triangle D B C, \triangle E C A, \triangle F A B$, 使得 $D 、 E 、 F$ 重合, 得到三棱雉. 当 $\triangle A B C$ 的 边长变化时, 所得三棱雉体积 (单位: $\mathrm{cm}^{3}$ ) 的最大值为