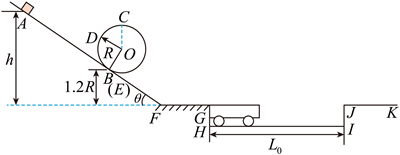
一游戏装置坚直截面如图所示, 该装置由固定在水平地面上倾角 $\theta=37^{\circ}$ 的直轨道 $A B$ 、螺旋圆形轨道 $B C D E$, 倾角 $\theta=37^{\circ}$ 的直轨道 $E F$ 、水平直轨道 $F G$ 组成, 除 $F G$ 段外各段轨道均光滑, 且各处平滑连 接。螺旋圆形轨道与轨道 $A B 、 E F$ 相切于 $B(E)$ 处. 凹槽 $G H I J$ 底面 $H I$ 水平光滑, 上面放有一无动力 摆渡车, 并紧靠在坚直侧壁 $G H$ 处, 摆渡车上表面与直轨道下 $F G$ 、平台 $J K$ 位于同一水平面。已知螺旋 圆形轨道半径 $R=0.5 \mathrm{~m}, B$ 点高度为 $1.2 R, F G$ 长度 $L_{F G}=2.5 \mathrm{~m}, H I$ 长度 $L_0=9 \mathrm{~m}$, 摆渡车长度 $L=3 \mathrm{~m}$ 、质量 $m=1 \mathrm{~kg}$ 。将一质量也为 $m$ 的滑块从倾斜轨道 $A B$ 上高度 $h=2.3 \mathrm{~m}$ 处静止释放, 滑块在 $F G$ 段运动时的阻力为其重力的 0.2 倍。(摆渡车碰到坚直侧壁 $I J$ 立即静止, 滑块视为质点, 不计空气阻 力, $\sin 37^{\circ}=0.6, \cos 37^{\circ}=0.8$ )
(1) 求滑块过 $C$ 点的速度大小 $v_C$ 和轨道对滑块的作用力大小 $F_C$;
(2) 摆渡车碰到 $I J$ 前, 滑块恰好不脱离摆渡车, 求滑块与摆渡车之间的动摩擦因数 $\mu$;
(3) 在 (2) 的条件下, 求滑块从 $G$ 到 $J$ 所用的时间 $t$ 。
(1) 求滑块过 $C$ 点的速度大小 $v_C$ 和轨道对滑块的作用力大小 $F_C$;
(2) 摆渡车碰到 $I J$ 前, 滑块恰好不脱离摆渡车, 求滑块与摆渡车之间的动摩擦因数 $\mu$;
(3) 在 (2) 的条件下, 求滑块从 $G$ 到 $J$ 所用的时间 $t$ 。
