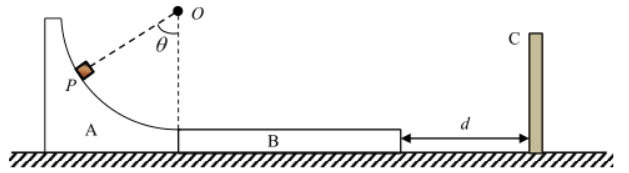
如图为某游戏装置的示意图, 由固定的坚直光滑圆弧轨道 $A$ 、静止在光滑水平面上的滑板 $B$ 、固定坚 直挡板 $C$ 组成。轨道 $A$ 的底端与滑板 $B$ 的上表面水平相切, 初始时轨道 $A$ 与滑板 $B$ 左端紧靠在一起, 滑板 $B$ 右端与竖直挡板 $C$ 相距 $d=$ $5 m$ 。游客乘坐滑椅 (可视为质点) 从轨道 $A$ 上 $P$ 点由静止出发, 冲上滑板 $B$, 滑板 $B$ 足够长 (滑椅不会从滑板表面滑出), 滑板 $B$ 与 挡板碰撞无机械能损失。已知游客与滑椅的总质量 $m=100 \mathrm{~kg}$, 圆弧轨道的半径 $R=6.4 \mathrm{~m}, O$ 点为圆弧轨道的圆心, $O P$ 与竖直方向夹 角 $60^{\circ}$, 滑板 $B$ 的质量 $M=300 \mathrm{~kg}$, 滑椅与滑板 $B$ 间的动摩擦因数 $\mu=0.2$, 空气阻力可忽略。求:
(1) 游客与滑椅滑到圆弧轨道最低点时的动量大小;
(2)滑板 $B$ 与竖直挡板碰撞前, 游客、滑椅和滑板 $B$ 组成的系统产生的内能;
(3) 若滑板 $B$ 右端与固定挡板 $C$ 距离 $d$ 可以改变, 并要求滑板 $B$ 只与挡板 $C$ 碰撞两次, 则 $d$ 应满足的条件。
(1) 游客与滑椅滑到圆弧轨道最低点时的动量大小;
(2)滑板 $B$ 与竖直挡板碰撞前, 游客、滑椅和滑板 $B$ 组成的系统产生的内能;
(3) 若滑板 $B$ 右端与固定挡板 $C$ 距离 $d$ 可以改变, 并要求滑板 $B$ 只与挡板 $C$ 碰撞两次, 则 $d$ 应满足的条件。
