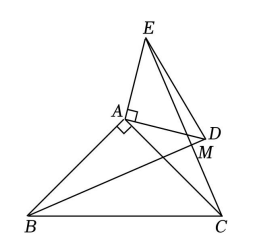
如图, $\triangle A B C$ 和 $\triangle A D E$ 是以点 $A$ 为直角顶点的等腰直角三角形, 把 $\triangle A D E$ 以 $A$ 为中心顺时针旋转, 点 $M$ 为射线 $B D 、 C E$ 的交点. 若 $A B=\sqrt{3}, A D=1$. 以下结论: (1) $B D=C E$; (2) $B D \perp C E$; (3)当点 $E$ 在 $B A$ 的延长线上时, $M C=\frac{3-\sqrt{3}}{2}$; (4)在旋转过程中, 当线段 $M B$ 最短时, $\triangle M B C$ 的面积为 $\frac{1}{2}$. 其中正确结论有

A. 1个
B. 2个
C. 3个
D. 4个