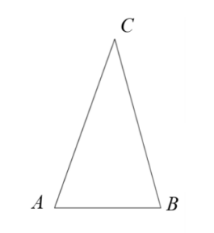
如图, 在 $\triangle A B C$ 中, $\angle C=35^{\circ}$, 将 $\triangle A B C$ 绕着点 $A$ 旋转 $\alpha\left(0^{\circ} < \alpha < 180^{\circ}\right)$, 旋转 后的点 $B$ 落在 $B C$ 上, 点 $B$ 的对应点为 $D$, 联结 $A D, A D$ 是 $\angle B A C$ 的角平分线, 则 $\alpha=$ 18. 在 $\triangle A B C$ 中, $A B=7, B C=3, \angle C=90^{\circ}$, 点 $D$ 在边 $A C$ 上, 点 $E$ 在 $C A$ 延长线上, 且 $C D=D E$, 如果 $\odot B$ 过点 $A, \odot E$ 过点 $D$, 若 $\odot B$ 与 $\odot E$ 有公共点, 那么 $\odot E$ 半径 $r$ 的取值范围是