阅读下列材料, 回答问题.
任务:测量一个扁平状的小水池的最大宽度,该水池东西走向的最大宽度
工具:一把皮尺 (测量长度略小于

小明利用皮尺测量, 求出了小水池的最大宽度
(i) 在小水池外选点
(ii) 分别在
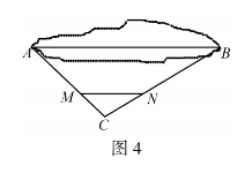
由测量知,
又
故小水池的最大宽度为
(1) 补全小明求解过程中(1)(2) 所缺的内容;
(2) 小明求得
(3) 小明仅利用皮尺, 通过 5 次测量,求得
要求: 测量得到的长度用字母
任务:测量一个扁平状的小水池的最大宽度,该水池东西走向的最大宽度
工具:一把皮尺 (测量长度略小于

小明利用皮尺测量, 求出了小水池的最大宽度
(i) 在小水池外选点
(ii) 分别在

由测量知,
又
故小水池的最大宽度为
(1) 补全小明求解过程中(1)(2) 所缺的内容;
(2) 小明求得
(3) 小明仅利用皮尺, 通过 5 次测量,求得
要求: 测量得到的长度用字母