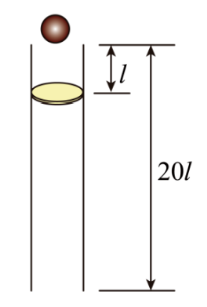
如图, 一坚直固定的长直圆管内有一质量为 $M$ 的静止薄圆盘, 圆盘与管的上端口距离 为 $l$, 圆管长度为 $20 l$ 。一质量为 $m=\frac{1}{3} M$ 的小球从管的上端口由静止下落, 并撞在圆盘 中心, 圆盘向下滑动, 所受滑动摩擦力与其所受重力大小相等。小球在管内运动时与管壁 不接触, 圆盘始终水平, 小球与圆盘发生的碰撞均为弹性碰撞且碰撞时间极短。不计空气 阻力, 重力加速度大小为 $g$ 。求
(1) 第一次碰撞后瞬涧小球和圆盘的速度大小;
(2)在第一次碰撞到第二次碰撞之间,小球与圆盘间的最远距离;
(3) 圆盘在管内运动过程中, 小球与圆盘碰撞的次数。
(1) 第一次碰撞后瞬涧小球和圆盘的速度大小;
(2)在第一次碰撞到第二次碰撞之间,小球与圆盘间的最远距离;
(3) 圆盘在管内运动过程中, 小球与圆盘碰撞的次数。
