如图,在正四棱杜 $A B C D-A_1 B_1 C_1 D_1$ 中, $A B=2, A A_1=4$. 点 $A_2, B_2, C_2, D_2$ 分别在棱 $A A_1, B B_1, C C_1, D D_1$ 上, $A A_2=1, B B_2=D D_2=2, C C_2=3$.
(1) 证明: $B_2 C_2 / / A_2 D_2$;
(2)点 $\mathrm{P}$ 在棱 $\mathrm{BB}_1$ 上,当二面角 $\mathrm{P}-\mathrm{A}_2 \mathrm{C}_2-\mathrm{D}_2$ 为 $150^{\circ}$ 时,求 $B_2 P$.
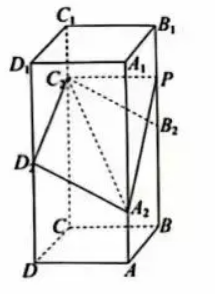
(1) 证明: $B_2 C_2 / / A_2 D_2$;
(2)点 $\mathrm{P}$ 在棱 $\mathrm{BB}_1$ 上,当二面角 $\mathrm{P}-\mathrm{A}_2 \mathrm{C}_2-\mathrm{D}_2$ 为 $150^{\circ}$ 时,求 $B_2 P$.
