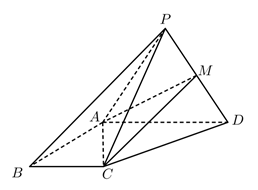
如图, 在四棱雉 $P-A B C D$ 中, 底面 $A B C D$ 为直角梯形, $\angle B A D=\angle C B A=\frac{\pi}{2}, P A=A D=$ $D P=A B=2, B C=1$, 平面 $P A D \perp$ 平面 $A B C D, M$ 为 $P D$ 的中点.
(1)证明: $C M \|$ 平面 $P A B$;
(2)求多面体 $P A B C M$ 的体积.

(1)证明: $C M \|$ 平面 $P A B$;
(2)求多面体 $P A B C M$ 的体积.