如图所示, 半径为 $R$ 光滑的 $\frac{1}{4}$ 圆弧轨道 $P A$ 固定安装在坚直平面内, $A$ 点的切线水平, 与水 平地面的高度差为 $R$, 让质量为 $m=0.2 \mathrm{~kg}$ 的小球甲 (视为质点) 从 $P$ 点由静止沿圆弧轨道滑 下, 从 $A$ 点飞出, 落在地面的 $B$ 点, 飞出后落到地面的水平位移为 $x=0.9 \mathrm{~m}$; 把质量为 $M=0.4 \mathrm{~kg}$ 的小球乙 (与甲的半径相同) 静止放置在 $A$ 点, 让小球田重新从 $P$ 点由静止沿圆弧轨道滑 下, 与乙发生弹性碰撞, 空气的阻力忽略不计、重力加速度 $g=10 \mathrm{~m} / \mathrm{s}^2$, 下列说法正确的是
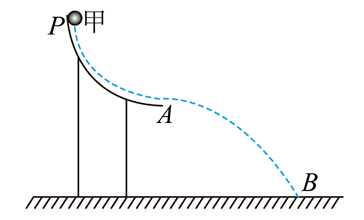

A. 圆弧轨道的半径 $R=0.9 \mathrm{~m}$
B. 乙从 $A$ 点飞出至落至地面过程中重力的冲量大小为 $0.6 \mathrm{~N} \cdot \mathrm{s}$
C. 甲、乙碰撞后乙的速度 $2.0 \mathrm{~m} / \mathrm{s}$
D. 乙对甲的冲量大小为 $1.2 \mathrm{~N} \cdot \mathrm{s}$