如图, 光滑平行轨道 $a b c d$ 的曲面部分是半径为 $R$ 的四分之一圆弧, 水平部分位于坚直向上、 大小为 $B$ 的匀强磁场中, 导轨部分两导轨间距为 $L$, 导轨II部分两导轨间距为 $\frac{L}{2}$, 将质量均 为 $m$ 的金属棒 $\mathrm{P}$ 和 $\mathrm{Q}$ 分别置于轨道上的 $a b$ 段和 $c d$ 段, 且与轨道垂直。 $\mathrm{P} 、 \mathrm{Q}$ 棒电阻均为 $r$, 导轨电阻不计。 $\mathrm{Q}$ 棒静止, 让 $\mathrm{P}$ 棒从圆弧最高点静止释放, 当 $\mathrm{P}$ 棒在导轨I部分运动时, $\mathrm{Q}$ 棒已达到稳定运动状态。下列说法正确的是
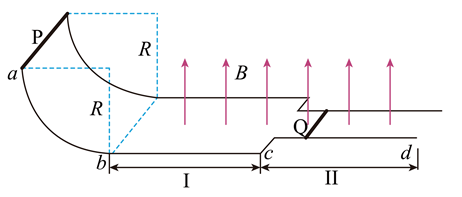

A. $\mathrm{P}$ 棒到达轨道最低点瞬间对轨道压力的大小为 $2 m g$
B. $\mathrm{Q}$ 棒第一次稳定运动时速度大小为 $\frac{\sqrt{2 g R}}{2}$
C. $\mathrm{Q}$ 棒从开始运动到第一次速度达到稳定, 该过程通过 $\mathrm{P}$ 棒的电荷量为 $\frac{4 m \sqrt{2 g R}}{5 B L}$
D. 从 $\mathrm{P}$ 棒进入导轨II云动到再次稳定过程中, $\mathrm{P} 、 \mathrm{Q}$ 棒中产生的总热量为 $\frac{1}{50} m g R$