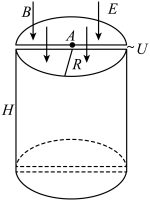
现有一对半圆柱体回旋加速器置于真空中, 如图所示, 其半径为 $R$, 高度为 $H$, 两金属盒 半圆柱体间狭缝宽度为 $d$, 有垂直于㑒面向下、磁感应强度大小为 $B$ 的匀强磁场和垂直于 盒面向下、电场强度大小为 $E$ 的匀强电场, 磁场仅存在于两盒内, 而电场存在于整个装 置, 两盒间接有电压为 $U$ 的交流电。加速器上表面圆心 $A$ 处有一粒子发射器, 现有一电荷 量为 $+q$ 、质量为 $m$ 的粒子从 $A$ 点飘入狭缝中, 初速度可以视为零。不考虑相对论效应和 重力作用, 若粒子能从加速器下表面边缘离开, 求:
(1) 若 $U$ 末知, 粒子从 $A$ 点到离开加速器下表面边缘所用时间 $t$ 及动能 $E_k$;
(2) 粒子在狹缝中被加速的次数 $n$;
(3) 若 $H$ 末知, 粒子在狭缝中被加速的时间与在磁场中运动的时间的比值。
(1) 若 $U$ 末知, 粒子从 $A$ 点到离开加速器下表面边缘所用时间 $t$ 及动能 $E_k$;
(2) 粒子在狹缝中被加速的次数 $n$;
(3) 若 $H$ 末知, 粒子在狭缝中被加速的时间与在磁场中运动的时间的比值。
