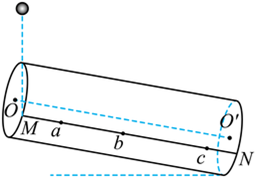
如图, 两端开口的圆筒与水平地面成一定角度倾斜放置。 $O O^{\prime}$ 是圆筒的中轴线, $M 、 N$ 是 筒壁上的两个点, 且 $M N / / O O^{\prime}$ 。一个可视为质点的小球自 $M$ 点正上方足够高处自由释 放, 由 $M$ 点无碰撞进入圆筒后一直沿筒壁运动, $a 、 b 、 c$ 是小球运动轨迹与 $M N$ 的交点。 小球从 $M$ 到 $a$ 用时 $t_1$, 从 $a$ 到 $b$ 用时 $t_2$, 从 $b$ 到 $c$ 用时 $t_3$, 小球经过 $a 、 b 、 c$ 时对筒壁压力 分别为 $F_a 、 F_b 、 F_c, l_{M a} 、 l_{a b} 、 l_{b c}$ 表示 $M 、 a 、 b 、 c$ 相邻两点间的距离, 不计一切摩擦。 下列说法正确的是

A. $t_1 < t_2 < t_3$
B. $F_a=F_b=F_c$
C. $F_a < F_b < F_c$
D. $l_{M a}: l_{a b}: l_{b c}=1: 3: 5$