如图所示, 间距为 $2 L$ 、倾角为 $\theta$ 的两足够长光滑金属导轨通过导线分别与半径为 $L$ 的光 滑水平金属圆轨道相连, 金属导轨上放置质量为 $m$ 、阻值为 $r$ 、长度为 $2 L$ 的导体棒 $a b$, 在圆轨道 上放置质量为 $m$ 、阻值为 $r$ 、长度为 $L$ 的导体棒 $O P$, 该导体棒可绕圆轨道的圆心 $O$ 自由转动, 两 区域均有垂直于所在轨道平面向上、磁感应强度大小为 $B$ 的匀强磁场。将位于斜轨道上的导体 棒由静止释放, $t_0$ 时间后, 该导体棒向下运动的距离为 $L_0$, 且两棒运动恰达到稳定状态。重力加 速度为 $g$, 已知圆轨道上导体棒的角加速度随时间的变化率与所受安培力的关系为 $a_{\varepsilon}=$ $\frac{3 F_{\mathrm{A}}}{2 m L}$, 求:
(1) 达到稳定状态时导体棒 $a b$ 的加速度 $a_1$ 的大小;
(2) 恰达到稳定状态时棒 $O P$ 转动的角速度 $\omega_0$ 。
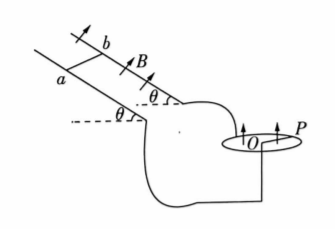
(1) 达到稳定状态时导体棒 $a b$ 的加速度 $a_1$ 的大小;
(2) 恰达到稳定状态时棒 $O P$ 转动的角速度 $\omega_0$ 。
