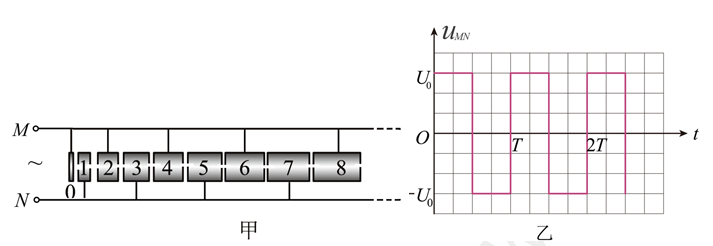
如图甲所示,某多级直线加速器由n个横截面积相同的金属圆筒依次排列,其中心轴线在同一直线上,各金属圆筒依序接在交变电源的两极M、N上,序号为C的金属圆板中央有一个质子源,质子逸出的速度不计,M、N两极加上如图乙所示的电压$u_{MN}$,一段时间后加速器稳定输出质子流。已知质子质量为m、电荷量为e,质子通过圆筒间隙的时间不计,且忽略相对论效应,则

A. 质子在各圆筒中做匀加速直线运动
B. 质子进入第 $n$ 个圆筒瞬间速度为 $\sqrt{\frac{2(n-1) e U_0}{m}}$
C. 各金属筒的长度之比为 $1: \sqrt{2}: \sqrt{3}: \cdots$
D. 质子在各圆筒中的运动时间之比为 $1: \sqrt{2}: \sqrt{3}: \cdots$