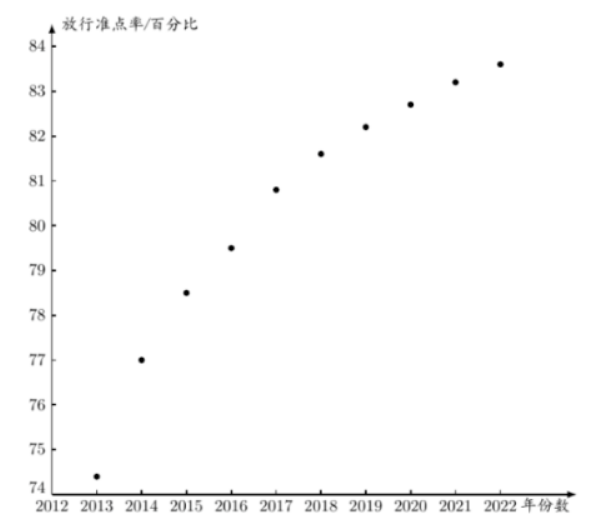
放行准点率是衡量机场运行效率和服务质量的重要指标之一. 某机场自 2012 年起采取相关策略优化 各个服务环节, 运行效率不断提升. 以下是根据近 10 年年份数 $x_i$ 与该机场飞往 $\mathrm{A}$ 地航班放行准点率 $y_i(i=1,2, \cdots, 10)$ (单位: 百分比) 的统计数据所作的散点图及经过初步处理后得到的一些统计量的值.
其中 $t_i=\ln \left(x_i-2012\right), \quad \bar{t}=\frac{1}{10} \sum_{i=1}^{10} t_i$.
(1) 根据散点图判断, $y=b x+a$ 与 $y=c \ln (x-2012)+d$ 哪一个适宜作为该机场飞往 A 地航班放行准 点率 $y$ 关于年份数 $x$ 的经验回归方程类型 (给出判断即可, 不必说明理由), 并根据表中数据建立经验回归 方程, 由此预测 2023 年该机场飞往 $\mathrm{A}$ 地的航班放行准点率.
(2) 已知 2023 年该机场飞往 A 地、B 地和其他地区的航班比例分别为 $0.2 、 0.2$ 和 0.6 . 若以 (1) 中 的预测值作为 2023 年该机场飞往 A 地航班放行准点率的估计值, 且 2023 年该机场飞往 B 地及其他地区 (不包含 A、B 两地) 航班放行准点率的估计值分别为 $80 \%$ 和 $75 \%$, 试解决以下问题:
(i) 现从 2023 年在该机场起飞的航班中随机抽取一个, 求该航班准点放行的概率;
(ii) 若 2023 年某航班在该机场准点放行, 判断该航班飞往 A 地、B 地、其他地区等三种情况中的哪 种情况的可能性最大, 说明你的理由.
附: (1) 对于一组数据 $\left(u_1, v_1\right),\left(u_2, v_2\right), \cdots,\left(u_n, v_n\right)$, 其回归直线 $v=\alpha+\beta u$ 的斜率和截距的最小二乘估计
分别为 $\hat{\beta}=\frac{\sum_{i=1}^n\left(u_i-\bar{u}\right)\left(v_i-\bar{v}\right)}{\sum_{i=1}^n\left(u_i-\bar{u}\right)^2}=\frac{\sum_{i=1}^n u_i v_i-n \bar{u}}{\sum_{i=1}^n u_i^2-n u^2}, \hat{\alpha}=\bar{v}-\hat{\beta} \bar{u}$;
(2) 参考数据: $\ln 10 \approx 2.30, \ln 11 \approx 2.40, \ln 12 \approx 2.48$.


其中 $t_i=\ln \left(x_i-2012\right), \quad \bar{t}=\frac{1}{10} \sum_{i=1}^{10} t_i$.
(1) 根据散点图判断, $y=b x+a$ 与 $y=c \ln (x-2012)+d$ 哪一个适宜作为该机场飞往 A 地航班放行准 点率 $y$ 关于年份数 $x$ 的经验回归方程类型 (给出判断即可, 不必说明理由), 并根据表中数据建立经验回归 方程, 由此预测 2023 年该机场飞往 $\mathrm{A}$ 地的航班放行准点率.
(2) 已知 2023 年该机场飞往 A 地、B 地和其他地区的航班比例分别为 $0.2 、 0.2$ 和 0.6 . 若以 (1) 中 的预测值作为 2023 年该机场飞往 A 地航班放行准点率的估计值, 且 2023 年该机场飞往 B 地及其他地区 (不包含 A、B 两地) 航班放行准点率的估计值分别为 $80 \%$ 和 $75 \%$, 试解决以下问题:
(i) 现从 2023 年在该机场起飞的航班中随机抽取一个, 求该航班准点放行的概率;
(ii) 若 2023 年某航班在该机场准点放行, 判断该航班飞往 A 地、B 地、其他地区等三种情况中的哪 种情况的可能性最大, 说明你的理由.
附: (1) 对于一组数据 $\left(u_1, v_1\right),\left(u_2, v_2\right), \cdots,\left(u_n, v_n\right)$, 其回归直线 $v=\alpha+\beta u$ 的斜率和截距的最小二乘估计
分别为 $\hat{\beta}=\frac{\sum_{i=1}^n\left(u_i-\bar{u}\right)\left(v_i-\bar{v}\right)}{\sum_{i=1}^n\left(u_i-\bar{u}\right)^2}=\frac{\sum_{i=1}^n u_i v_i-n \bar{u}}{\sum_{i=1}^n u_i^2-n u^2}, \hat{\alpha}=\bar{v}-\hat{\beta} \bar{u}$;
(2) 参考数据: $\ln 10 \approx 2.30, \ln 11 \approx 2.40, \ln 12 \approx 2.48$.
