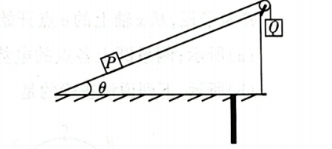
如图, 小物块 $P$ 置于倾角 $\theta=30^{\circ}$ 的光滑固定斜面上, 轻质定滑轮固定在斜面顶端, $Q$ 和 $P$ 用跨过定滑轮的不可伸长的轻绳相连, 轻绳恰好和斜面平行。 $t=0$ 时将 $P$ 由静止释 放, 此时 $Q$ 的加速度大小为 $\frac{g}{4}$ 。 $t_0$ 时刻轻绳突然断裂, 之后 $P$ 能达到的最高点恰与 $Q$ 被 释放时的位置处于同一高度。取 $t=0$ 时 $P$ 所在水平面为零势能面, 此时 $Q$ 的机械能为 $E$ 。已知 $0 \sim 2 t_0$ 内 $Q$ 末落地,不考虑空气阻力,下列说法正确的是

A. $P 、 Q$ 质量之比为 $1: 2$
B. $\frac{3 t_0}{2}$ 时 $Q$ 的机械能为 $\frac{E}{2}$
C. $\frac{3 t_0}{2}$ 时 $P$ 的重力势能为 $E$
D. $2 t_0$ 时 $P$ 重力的功率为 $\frac{2 E}{3 t_0}$