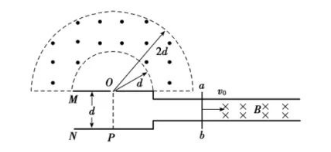
如图所示, 间距为 $d$ 的平行金属板 $M N$ 与一对光滑的平行导轨相连, 平行导轨间距为 $L$. 一根导体棒 $a b$ 与导轨垂直且以速度 $v_0$ 沿导轨向右匀速运动, 棒的右側存在一个垂直纸面向里, 大小为 $B$ 的匀强磁场. 当棒进入磁场时, 粒子源 $P$ 释放一个初速度为零的带负电的粒子, 已知带电粒子的质量为 $m$ (重力不计), 电量为 $q$.粒子经电场加速后从 $M$ 板上的小孔 $O$ 穿出. 在板的上方, 有一个环形区域内存在垂直纸面向外的匀强磁场. 已知外圆半怪为 $2 d$, 内圆半径为 $d$, 两圆的圆心与小孔重合 ,
求:
(1)粒子到达 $M$ 板的速度大小 $v$;
(2)若粒子不能从外圆边界飞出, 则环形区域内磁感应强度最小为多少?
求:

(1)粒子到达 $M$ 板的速度大小 $v$;
(2)若粒子不能从外圆边界飞出, 则环形区域内磁感应强度最小为多少?