为提高学生的数学应用能力和创造力, 学校打算开设 “数学建模” 选修课, 为了解学 生对 “数学建模” 的兴趣度是否与性别有关, 学校随机抽取该校 30 名高中学生进行问卷调查, 其中认为感兴趣的人数占 $70 \%$.
(1) 根据所给数据, 完成下面的 $2 \times 2$ 列联表, 并根据列联表判断是否有 $85 \%$ 的把握认为学生对
“数学建模” 选修课的兴趣度与性别有关?
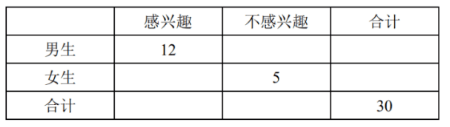
若感兴趣的女生中恰有 4 名是高三学生, 现从感兴趣的女生中随机选出 3 名进行二次访谈, 记选出高三女生的人数为 $X$, 求 $X$ 的分布列与数学期望.
$$
\text { 附: } K^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)} \text {, 其中 } n=a+b+c+d \text {. }
$$

(1) 根据所给数据, 完成下面的 $2 \times 2$ 列联表, 并根据列联表判断是否有 $85 \%$ 的把握认为学生对
“数学建模” 选修课的兴趣度与性别有关?

若感兴趣的女生中恰有 4 名是高三学生, 现从感兴趣的女生中随机选出 3 名进行二次访谈, 记选出高三女生的人数为 $X$, 求 $X$ 的分布列与数学期望.
$$
\text { 附: } K^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)} \text {, 其中 } n=a+b+c+d \text {. }
$$
