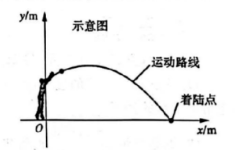
原地正面掷实心球是中招体育者试项目之一. 受测者站在起掷线后, 被掷出的实心球进行斜抛运动, 实心球着陆点到起掷线的距离即为此项目成绩. 实心球的运动轨迹可看作抛物线的一部分. 如图,建立平面直角坐标系, 实心球从出手到着陆的过程中, 竖直高度 $y(\mathrm{~m})$ 与水平距离 $x(\mathrm{~m})$ 近似满足函数关系 $y=$ $a x^2+b x+c(a < 0)$. 小明使用内置传感器的智能实心球进行掷实心球训练.
(1)第一次训练时,智能实心球回传的水平距离 $x(\mathrm{~m})$ 与竖直高度 $y(\mathrm{~m})$ 的 几组对应数据如下:

则,
①抛物线顶点的坐标是 , 顶点坐标的实际意义是
② 求 $y$ 与 $x$ 近似满足的函数关系式,并直接写出本次训练的成绩
(2)第二次训练时, $y$ 与 $x$ 近似涑足函数关系 $y=-0.09 x^2+0.72 x+1.8$, 则第二火训练成绩与第一次相比是否有提啇? 为什么?
(3)实心球的抛物线轨迹是影响成绩的重要因素, 可以通过多种方法调整实心球的轨迹。 小明掷实心球的出手高度不变,即抛物线 $y=ax^2+bx+c (a < 0 )$
中 $c$ 的值不变, 要㧹高成绩应使 $a, b$ 的值做怎样的调整?

(1)第一次训练时,智能实心球回传的水平距离 $x(\mathrm{~m})$ 与竖直高度 $y(\mathrm{~m})$ 的 几组对应数据如下:

则,
①抛物线顶点的坐标是 , 顶点坐标的实际意义是
② 求 $y$ 与 $x$ 近似满足的函数关系式,并直接写出本次训练的成绩
(2)第二次训练时, $y$ 与 $x$ 近似涑足函数关系 $y=-0.09 x^2+0.72 x+1.8$, 则第二火训练成绩与第一次相比是否有提啇? 为什么?
(3)实心球的抛物线轨迹是影响成绩的重要因素, 可以通过多种方法调整实心球的轨迹。 小明掷实心球的出手高度不变,即抛物线 $y=ax^2+bx+c (a < 0 )$
中 $c$ 的值不变, 要㧹高成绩应使 $a, b$ 的值做怎样的调整?