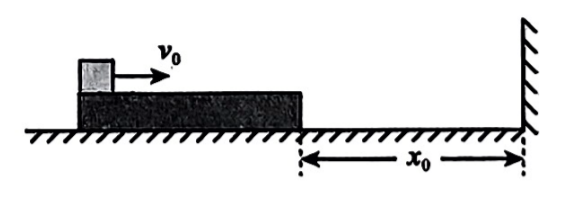
如图所示, 足够长的木板静止放在光滑水平面上, 木板右端与墙壁相距为 $x_0=0.5 \mathrm{~m}$, 在木板左端放一个质量为 $m$ 的小物块 (可视为质点), 与木板的动摩擦因数为 $\mu=0.2$, 木板的质量为 $M, m=2 M$, 现给小物块一个水平向右的初始速度 $v_0=3 \mathrm{~m} / \mathrm{s}$, 运动过程 中, 木板与墙壁发生弹性碰撞 (碰撞后原速率反弹), 重力加速度为 $g=10 \mathrm{~m} / \mathrm{s}^2$ 。在 整个运动过程中, 下列说法正确的是

A. 木板碰墙前, 木块的速度大于木板速度
B. 木板向左运动的最大距离为 $0.5 \mathrm{~m}$
C. 木板的总路程为 $1.5 \mathrm{~m}$
D. 木板的总路程为 $\frac{13}{8} \mathrm{~m}$