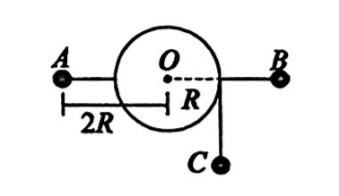
如图所示, 鼓形轮的半径为 $R$, 可绕固定的光滑水平轴 $O$ 转动。在轮上沿直径方向固 定两根直杆, 杆上分别固定有小球 $A 、 B$, 两球与 $O$ 的距离均为 $2 R$ 。在轮上绕有长绳, 绳上悬挂着小球 $C$ 。已知三个小球质量相等, 绳与轮之间无相对滑动, 忽略鼓形轮、 直杆和长绳的质量, 不计空气阻力, 重力加速度为 $g$ 。开始 $A 、 B$ 两小球与鼓形轮圆心 等高, 两球从静止开始运动, 带动鼓形轮转动。在 $B$ 球顺时针转动到最低位置的过程 中 (三球在转动过程中不相碰)。以下说法正确的是

A. 同一时刻 $A$ 球的角速度大小是 $C$ 球的两倍
B. 重力对 $B$ 球做功的瞬时功率一直增大
C. 杆对 $B$ 球不做功, $B$ 球机械能守恒
D. $B$ 球转动到最低位置时的速度大小为 $v=\frac{2}{3} \sqrt{\pi g R}$