过四边形 $A B C D$ 的顶点 $A$ 作射线 $A M, P$ 为射线 $A M$ 上一点, 连接 $D P$. 将 $A P$ 绕点 $A$ 顺时针方向旋转至 $A Q$, 记旋转角 $\angle P A Q=\alpha$, 连接 $B Q$.
(1)【探究发现】如图 1, 数学兴趣小组探究发现, 如果四边形 $A B C D$ 是正方形, 且 $\alpha=90^{\circ}$. 无论点 $P$ 在何处, 总有 $B Q=D P$, 请证明这个结论.
(2)【类比迁移】如图 2, 如果四边形 $A B C D$ 是菱形, $\angle D A B=\alpha=60^{\circ}, \angle M A D=15^{\circ}$, 连接 $P Q$. 当 $P Q \perp B Q, A B=\sqrt{6}+\sqrt{2}$ 时, 求 $A P$ 的长;
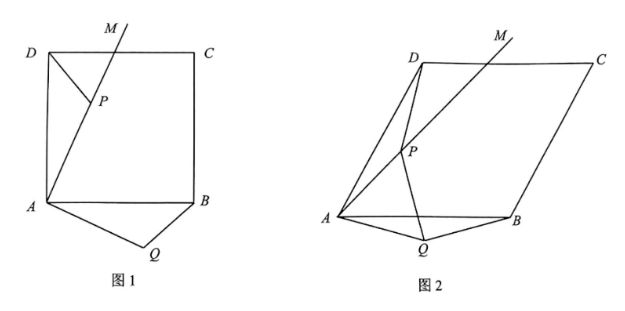
(3)【拓展应用】如图 3, 如果四边形 $A B C D$ 是矩形, $A D=6, A B=8, A M$ 平分 $\angle D A C$, $\alpha=90^{\circ}$. 在射线 $A Q$ 上截取 $A R$, 使得 $A R=\frac{4}{3} A P$. 当 $\triangle P B R$ 是直角三角形时, 请直 接写出 $A P$ 的长.
(1)【探究发现】如图 1, 数学兴趣小组探究发现, 如果四边形 $A B C D$ 是正方形, 且 $\alpha=90^{\circ}$. 无论点 $P$ 在何处, 总有 $B Q=D P$, 请证明这个结论.
(2)【类比迁移】如图 2, 如果四边形 $A B C D$ 是菱形, $\angle D A B=\alpha=60^{\circ}, \angle M A D=15^{\circ}$, 连接 $P Q$. 当 $P Q \perp B Q, A B=\sqrt{6}+\sqrt{2}$ 时, 求 $A P$ 的长;

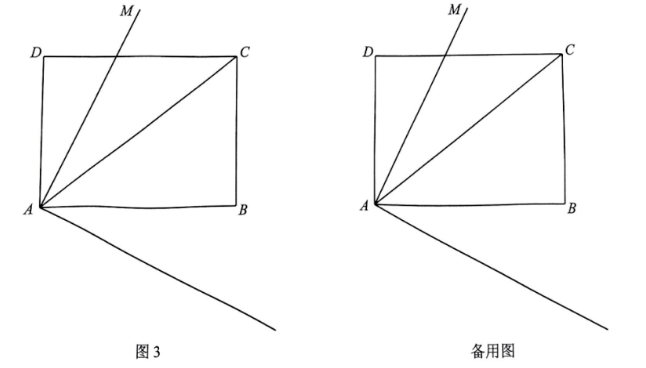
(3)【拓展应用】如图 3, 如果四边形 $A B C D$ 是矩形, $A D=6, A B=8, A M$ 平分 $\angle D A C$, $\alpha=90^{\circ}$. 在射线 $A Q$ 上截取 $A R$, 使得 $A R=\frac{4}{3} A P$. 当 $\triangle P B R$ 是直角三角形时, 请直 接写出 $A P$ 的长.
