已知函数 $f(x)=2 \sin (\omega x+\varphi)\left(\omega \in \mathbf{N}^*, 0 < \varphi < \frac{\pi}{2}\right)$ 的部分图象如图所示, 且函数 $f(x)$ 在 $x=\frac{7 \pi}{12}$ 处取得最小值, 则函数 $f\left(\frac{x}{2}\right)$ 在 $[0, \pi]$ 上的单调递减区间为
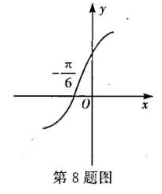

A. $\left[0, \frac{\pi}{6}\right]$
B. $\left[\frac{\pi}{6}, \frac{5 \pi}{6}\right]$
C. $\left[0, \frac{\pi}{12}\right]$
D. $\left[\frac{\pi}{6}, \pi\right]$