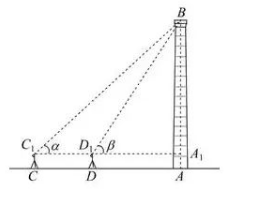
某建筑物如图所示, 底部为 $\mathrm{A}$, 顶部为 $B$, 点 $C, D$ 与点 $\mathrm{A}$ 在同一水平线上, 且 $|C D|=l$, 用高为 $h$ 的测角工具在 $C, D$ 位置测得建筑物顶部 $B$ 在 $C_1$ 和 $D_1$处的仰角分别为 $\alpha, \beta$. 其中 $C_1, D_1$ 和 $\mathrm{A}_1$ 在同一条水平线上, $A_1$ 在 $A B$ 上, 则该建筑物的高 $A B=(\quad)$

A. $\frac{l \sin \alpha \cos \beta}{\sin (\beta-\alpha)}+h$
B. $\frac{l \cos \alpha \cos \beta}{\sin (\beta-\alpha)}+h$
C. $\frac{l \cos \alpha \sin \beta}{\sin (\beta-\alpha)}+h$
D. $\frac{l \sin \alpha \sin \beta}{\sin (\beta-\alpha)}+h$