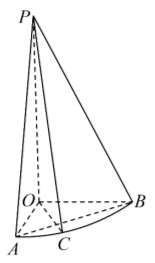
如图, 在直角 $\triangle P O A$ 中, $P O \perp O A, P O=2 O A=4$, 将 $\triangle P O A$ 绕边 $P O$ 旋转到 $\triangle P O B$ 的位置, 使 $\angle A O B=90^{\circ}$, 得到圆雉的一部分, 点 $C$ 为 $\overparen{A B}$ 上的点, 且 $\overparen{A C}=\frac{1}{3} \overparen{A B}$.
(1) 求点 $O$ 到平面 $P A B$ 的距离;
(2) 设直线 $P C$ 与平面 $P A B$ 所成的角为 $\varphi$, 求 $\sin \varphi$ 的值.
(1) 求点 $O$ 到平面 $P A B$ 的距离;
(2) 设直线 $P C$ 与平面 $P A B$ 所成的角为 $\varphi$, 求 $\sin \varphi$ 的值.
