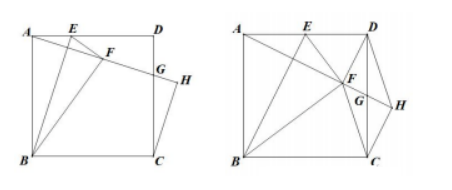
如图 1, 在正方形 $A B C D$ 中, 点 $E$ 是边 $A D$ 上一动点, 把 $\triangle A B E$ 沿 $B E$ 折叠得到 $\triangle F B E$, 连接 $A F$ 并延长, 交 $C D$ 于点 $G$, 过 $C$ 作 $C H \perp A F$ 于点 $H$.
(1) 证明: $\angle B F H=\angle B C H$;
(2) 如图 2, 若点 $E$ 是 $A D$ 中点, 连接 $D F, C F, D H$, 证明:四边形 $D F C H$ 是平行四边形:
(3) 点 $E$ 在运动过程中, $\frac{A H}{A G}$ 是否存在最大值? 如果存在, 请把它求出来; 如果不存在, 请说明理由.
(1) 证明: $\angle B F H=\angle B C H$;
(2) 如图 2, 若点 $E$ 是 $A D$ 中点, 连接 $D F, C F, D H$, 证明:四边形 $D F C H$ 是平行四边形:
(3) 点 $E$ 在运动过程中, $\frac{A H}{A G}$ 是否存在最大值? 如果存在, 请把它求出来; 如果不存在, 请说明理由.
