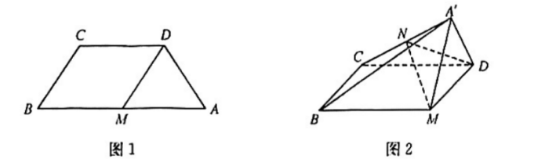
如图 1, 四边形 $A B C D$ 是梯形, $A B / / C D, A D=D C=C B=\frac{1}{2} A B=4, M$ 是 $A B$ 的中点, 将 $\triangle A D M$ 沿 $D M$ 折起至 $\triangle A^{\prime} D M$, 如图 2, 点 $N$ 在线段 $A^{\prime} C$ 上.
(1) 若 $N$ 是 $A^{\prime} C$ 的中点, 求证: 平面 $D N M \perp$ 平面 $A^{\prime} B C$;
(2) 若 $A^{\prime} C=2 \sqrt{6}$, 平面 $D N M$ 与平面 $C D M$ 夹角的余弦值为 $\frac{2 \sqrt{5}}{5}$, 求 $\frac{A^{\prime} N}{N C}$.

(1) 若 $N$ 是 $A^{\prime} C$ 的中点, 求证: 平面 $D N M \perp$ 平面 $A^{\prime} B C$;
(2) 若 $A^{\prime} C=2 \sqrt{6}$, 平面 $D N M$ 与平面 $C D M$ 夹角的余弦值为 $\frac{2 \sqrt{5}}{5}$, 求 $\frac{A^{\prime} N}{N C}$.