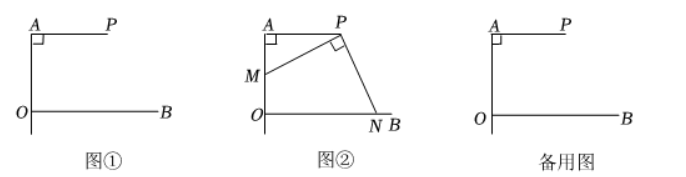
如图, $\angle A O B=90^{\circ}$, 点 $P$ 在 $\angle A O B$ 的平分线上, $P A \perp O A$ 于点 $A$.
(1)【操作判断】
如图(1), 过点 $P$ 作 $P C \perp O B$ 于点 $C$ ,根据题意在图(1)中画出 $P C$ ,图中 $\angle A P C$ 的度数为 90 度;
(2)【问题探究】
如图(2), 点 $M$ 在线段 $A O$ 上, 连接 $P M$, 过点 $P$ 作 $P N \perp P M$ 交射线 $O B$ 于点 $N$, 求证: $O M+O N=2 P A$ ;
(3)【拓展延伸】
点 $M$ 在射线 $A O$ 上, 连接 $P M$, 过点 $P$ 作 $P N \perp P M$ 交射线 $O B$ 于点 $N$, 射线 $N M$ 与射线 $P O$ 相交于点 $F$, 若 $O N=3 O M$, 求 $\frac{O P}{O F}$ 的值.
(1)【操作判断】
如图(1), 过点 $P$ 作 $P C \perp O B$ 于点 $C$ ,根据题意在图(1)中画出 $P C$ ,图中 $\angle A P C$ 的度数为 90 度;
(2)【问题探究】
如图(2), 点 $M$ 在线段 $A O$ 上, 连接 $P M$, 过点 $P$ 作 $P N \perp P M$ 交射线 $O B$ 于点 $N$, 求证: $O M+O N=2 P A$ ;
(3)【拓展延伸】
点 $M$ 在射线 $A O$ 上, 连接 $P M$, 过点 $P$ 作 $P N \perp P M$ 交射线 $O B$ 于点 $N$, 射线 $N M$ 与射线 $P O$ 相交于点 $F$, 若 $O N=3 O M$, 求 $\frac{O P}{O F}$ 的值.
