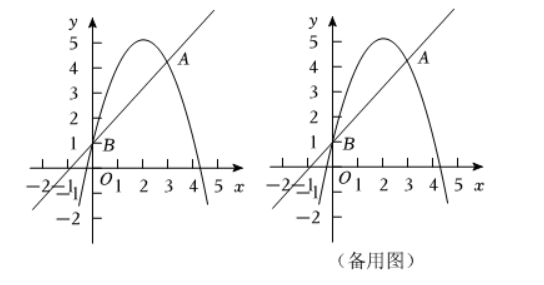
如图, 在平面直角坐标系中, 已知抛物线 $y=-x^2+b x+c$ 与直线相交于 $A, B$ 两点, 其中点 $A(3,4), B(0,1)$.
(1) 求该抛物线的函数解析式;
(2)过点 $B$ 作 $B C \| x$ 轴交抛物线于点 $C$. 连接 $A C$ ,在抛物线上是否存在点 $P$ 使 $\tan \angle B C P=\frac{1}{6} \tan \angle A C B$. 若存在,请求出满足条件的所有点 $P$ 的坐标;若不存在,请说明理由。(提示:依题意补全图形,并解答)
(3) 将该抛物线向左平移 2 个单位长度得到 $y_1=a_1 x^2+b_1 x+c_1\left(a_1 \neq 0\right)$, 平移后的抛物线与原抛物线相交于点 $D$, 点 $E$ 为原抛物线对称轴上的一点, $F$ 是平面直角坐标系内的一点, 当以点 $B, D, E, F$ 为顶点的四边形是菱形时, 请直接写出点 $F$ 的坐标.
(1) 求该抛物线的函数解析式;
(2)过点 $B$ 作 $B C \| x$ 轴交抛物线于点 $C$. 连接 $A C$ ,在抛物线上是否存在点 $P$ 使 $\tan \angle B C P=\frac{1}{6} \tan \angle A C B$. 若存在,请求出满足条件的所有点 $P$ 的坐标;若不存在,请说明理由。(提示:依题意补全图形,并解答)
(3) 将该抛物线向左平移 2 个单位长度得到 $y_1=a_1 x^2+b_1 x+c_1\left(a_1 \neq 0\right)$, 平移后的抛物线与原抛物线相交于点 $D$, 点 $E$ 为原抛物线对称轴上的一点, $F$ 是平面直角坐标系内的一点, 当以点 $B, D, E, F$ 为顶点的四边形是菱形时, 请直接写出点 $F$ 的坐标.
