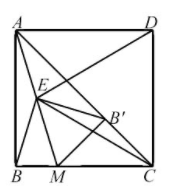
如图, 正方形 $A B C D$ 中, 点 $M$ 在边 $B C$ 上, 点 $E$ 是 $A M$ 的中点,连接 $E D, E C$.
(1) 求证: $E D=E C$.
(2) 将 $B E$ 绕点 $E$ 逆时针旋转, 使点 $B$ 的对应点 $B$ 落在 $A C$ 上,连接 $M B^{\prime}$. 当点 $M$ 在边 $B C$ 上运动时 (点 $M$ 不与 $B, C$ 重合),判断 $\triangle C M B^{\prime}$ 的形状, 并说明理由.
(3) 在 (2) 的条件下, 已知 $A B=1$, 当 $\angle D E B^{\prime}=45^{\circ}$ 时, 求 $B M$的长.
(1) 求证: $E D=E C$.
(2) 将 $B E$ 绕点 $E$ 逆时针旋转, 使点 $B$ 的对应点 $B$ 落在 $A C$ 上,连接 $M B^{\prime}$. 当点 $M$ 在边 $B C$ 上运动时 (点 $M$ 不与 $B, C$ 重合),判断 $\triangle C M B^{\prime}$ 的形状, 并说明理由.
(3) 在 (2) 的条件下, 已知 $A B=1$, 当 $\angle D E B^{\prime}=45^{\circ}$ 时, 求 $B M$的长.
