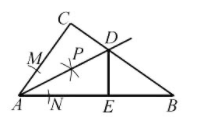
如图, 在 Rt $\triangle A B C$ 中, $\angle C=90^{\circ}, A C=6, A B=10$. 以点 $A$ 为圆心, 适当长为半径画弧, 分别交 $A C, A B$ 于点 $M, N$, 再分别以 $M, N$ 为圆心, 大于 $\frac{1}{2} M N$ 的长为半径两弧, 两弧在 $\angle C A B$的内部相交于点 $P$, 画射线 $A P$ 与 $B C$ 交于点 $D, D E \perp A B$, 垂足为 $E$. 则下列结论错误的是

A. $\angle C A D=\angle B A D$
B. $C D=D E$
C. $A D=5 \sqrt{3}$
D. $C D: B D=3: 5$