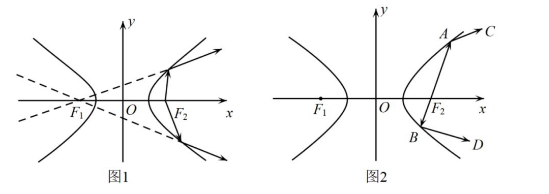
如图 1 所示, 双曲线具有光学性质; 从双曲线右焦点发出的光线经过双曲线镜面反射, 其反射光线的反 向延长线经过双曲线的左焦点. 若双曲线 $E: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1(a>0, b>0)$ 的左、右焦点分别为 $F_{1}, F_{2}$, 从 $F_{2}$ 发 出的光线经过图 2 中的 $A, B$ 两点反射后, 分别经过点 $C$ 和 $D$, 且 $\cos \angle B A C=-\frac{3}{5}, A B \perp B D$, 则 $E$ 的 离心率为()

A. $\frac{\sqrt{5}}{2}$
B. $\frac{\sqrt{17}}{3}$
C. $\frac{\sqrt{10}}{2}$
D. $\sqrt{5}$