某工厂进行生产线智能化升级改造. 升级改造后, 从该工厂甲、乙两个车间的产品中随机抽取 150 件进行检验, 数据如下:
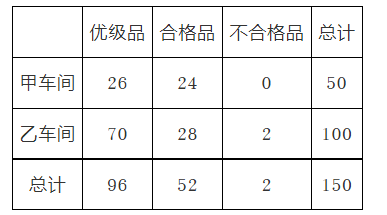
(1)填写如下联保表

能否有 $95 \%$ 的把握认为甲、乙两车间产品的优级品率存在差异? 能否有 $99 \%$ 的把握认为甲、乙两车间产品的优级品率存在差异?
(2) 已知升级改造前该工厂产品的优级品率 $p=0.5$. 设 $\bar{p}$ 为升级改造后抽取的 $n$ 件产品的优级品率. 如果 $\bar{p}>p+1.65$
$\sqrt{\frac{p(1-p)}{n}}$, 则认为该工厂产品的优级品率提高了. 根据抽取的 150 件产品的数据, 能否认为生产线智能化升级改造后, 该工厂产品的优级品率提高了? $(\sqrt{150} \approx 12.247$ )
附: $K^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$,


(1)填写如下联保表

能否有 $95 \%$ 的把握认为甲、乙两车间产品的优级品率存在差异? 能否有 $99 \%$ 的把握认为甲、乙两车间产品的优级品率存在差异?
(2) 已知升级改造前该工厂产品的优级品率 $p=0.5$. 设 $\bar{p}$ 为升级改造后抽取的 $n$ 件产品的优级品率. 如果 $\bar{p}>p+1.65$
$\sqrt{\frac{p(1-p)}{n}}$, 则认为该工厂产品的优级品率提高了. 根据抽取的 150 件产品的数据, 能否认为生产线智能化升级改造后, 该工厂产品的优级品率提高了? $(\sqrt{150} \approx 12.247$ )
附: $K^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$,
