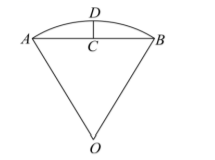
沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”, 如图, $A B$ 是以 $O$ 为圆心, $O A$ 为半径的圆弧, $C$ 是 $A B$ 的中点, $D$ 在 $A B$ 上, $C D \perp A B$. “会圆术"给出 $A B$ 的弧长的近似值 $s$ 的计算公式: $s=A B+\frac{C D^2}{O A}$. 当 $O A=2, \angle A O B=60^{\circ}$ 时, $s=$

A. $\frac{11-3 \sqrt{3}}{2}$
B. $\frac{11-4 \sqrt{3}}{2}$
C. $\frac{9-3 \sqrt{3}}{2}$
D. $\frac{9-4 \sqrt{3}}{2}$