已知函数 $f(x)=\sin \omega x+a \cos \omega x \quad(x \in \mathbf{R}, \omega>0)$ 的最大值为 2 , 其部分图象如图所示, 则
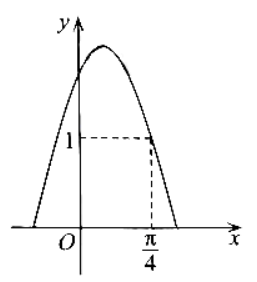

A. $a=\sqrt{3}$
B. 函数 $f\left(x-\frac{\pi}{6}\right)$ 为偶函数
C. 满足条件的正实数 $\omega$, 存在且唯一
D. $f(x)$ 是周期函数, 且最小正周期为 $\pi$