(1)设总体X具有分布率
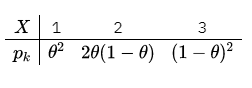
其中
(2)设
(3)设随机变量
其中
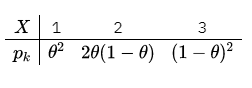
其中
(2)设
(3)设随机变量
其中