甲、乙、丙三人进行投篮比赛, 共比赛 10 场, 规定每场比赛分数最高者获胜, 三人得分 (单位:
分)情况统计如下:
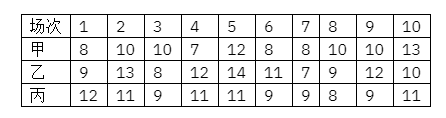
(1)从上述 10 场比赛中随机选择一场,求甲获胜的概率;
(2)在上述 10 场比赛中, 从甲得分不低于 10 分的场次中随机选择两场, 设 $X$ 表示乙得分大于丙得分的场数, 求 $X$ 的分布列和数学期望 $E(X)$;
(3)假设每场比赛获胜者唯一, 且各场相互独立, 用上述 10 场比赛中每人获胜的频率估计其获胜的概率. 甲、乙、丙三人接下来又将进行 6 场投篮比赛, 设 $Y_1$ 为甲获胜的场数, $Y_2$ 为乙获胜的场数, $Y_3$ 为丙获胜的场数, 写出方差 $D\left(Y_1\right), D\left(Y_2\right), D\left(Y_3\right)$ 的大小关系.
分)情况统计如下:

(1)从上述 10 场比赛中随机选择一场,求甲获胜的概率;
(2)在上述 10 场比赛中, 从甲得分不低于 10 分的场次中随机选择两场, 设 $X$ 表示乙得分大于丙得分的场数, 求 $X$ 的分布列和数学期望 $E(X)$;
(3)假设每场比赛获胜者唯一, 且各场相互独立, 用上述 10 场比赛中每人获胜的频率估计其获胜的概率. 甲、乙、丙三人接下来又将进行 6 场投篮比赛, 设 $Y_1$ 为甲获胜的场数, $Y_2$ 为乙获胜的场数, $Y_3$ 为丙获胜的场数, 写出方差 $D\left(Y_1\right), D\left(Y_2\right), D\left(Y_3\right)$ 的大小关系.