在平面直角坐标系中, 点 $P(a, b), Q(c, d)$ 给出如下定义:对于实数 $k(k \neq 0)$, 我们称点 $M(k a$ $+k c, k b+k d)$ 为 $P, Q$ 两点的“ $k$ ” 系和点. 例如, 点 $P(3,4), Q(1,-2)$, 则点 $P, Q$ 的“$\frac{1}{2}$”系和点的坐标为: $(2,1)$.
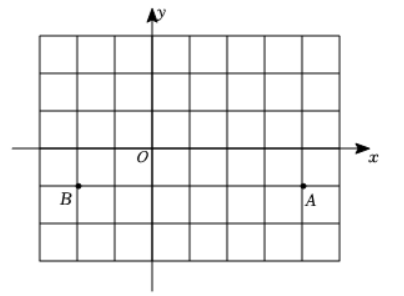
(1) 如图, 已知点 $A(4,-1), B(-2,-1)$.
①直接写出点 $A, B$ 的 “ $-\frac{1}{2}$ ”系和点坐标为
②若点 $A$ 为 $B, C$ 的 “ -3 ”系和点, 求点 $C$ 的坐标;
( 2 ) 已知点 $P(1-a,-2 m), Q(b,-2 m), P$ 在第四象限, 直线 $P Q$ 交 $y$ 轴于点 $E$, 点 $M(5 m+2,-4 m)$ 是 $P, Q$ 的“ 1 ”系和点, 将线段 $P Q$ 平移到 $M N$ ( $P$ 与 $M$ 对应, $Q$ 与 $N$ 对应 ), 且 $N(4 m+2, n)$, 直线 $M N$ 交 $y$ 轴于点 $F, G$ 为 $x$ 轴正半轴上一点, 且 $S_{\triangle G E F}=4 m^2+2 m$. 问: 是否存在 $m$, 使得 $S_{\triangle E G N}=3 S_{\triangle P G N}$, 若存在, 求出 $m$ 的值, 若不存在, 说明理由.

(1) 如图, 已知点 $A(4,-1), B(-2,-1)$.
①直接写出点 $A, B$ 的 “ $-\frac{1}{2}$ ”系和点坐标为
②若点 $A$ 为 $B, C$ 的 “ -3 ”系和点, 求点 $C$ 的坐标;
( 2 ) 已知点 $P(1-a,-2 m), Q(b,-2 m), P$ 在第四象限, 直线 $P Q$ 交 $y$ 轴于点 $E$, 点 $M(5 m+2,-4 m)$ 是 $P, Q$ 的“ 1 ”系和点, 将线段 $P Q$ 平移到 $M N$ ( $P$ 与 $M$ 对应, $Q$ 与 $N$ 对应 ), 且 $N(4 m+2, n)$, 直线 $M N$ 交 $y$ 轴于点 $F, G$ 为 $x$ 轴正半轴上一点, 且 $S_{\triangle G E F}=4 m^2+2 m$. 问: 是否存在 $m$, 使得 $S_{\triangle E G N}=3 S_{\triangle P G N}$, 若存在, 求出 $m$ 的值, 若不存在, 说明理由.