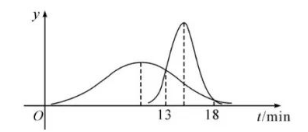
小明上学有时坐公交车, 有时骑自行车, 他各记录了 10 次坐公交车和骑自行车所花的时间, 10 次坐公交车所花的时间分别为 $7,11,8,12,8,13,6,13,7,15$ (单位: $\mathrm{min}$ ), 10 次骑自行车所花时间的均值为 $15 \mathrm{~min}$, 方差为 1 . 已知坐公交车所花时间 $X$ 与骑自行车所花时间 $Y$ 都服从正态分布,用样本均值和样本方差估计 $X, Y$ 分布中的参数,并利用信息技术工具画出 $X$ 和 $Y$ 的分布密度曲线如图所示. 若小明每天需在早上 8 点之前到校, 否则就迟到, 则下列判断正确的是

A. 坐公交车所花时间的均值为 10 ,方差为 3
B. 若小明早上 $7: 50$ 之后出发, 并选择坐公交车, 则有 $50 \%$ 以上的可能性会迟到
C. 若小明早上 $7: 42$ 出发,则应选择骑自行车
D. 若小明早上 $7: 47$ 出发,则应选择坐公交车