已知直三棱柱 $A B C-A_1 B_1 C_1$ 中, 侧面 $A A_1 B_1 B$ 为正方形, $A B=B C=2, E, F$ 分别为 $A C$ 和 $C C_1$ 的中点, $D$ 为棱 $A_1 B_1$ 上的点, 设 $B_1 D=m, B F \perp A_1 B_1$.
(1) 证明: $B F \perp D E$;
(2) 当 $m$ 为何值时, 平面 $B B_1 C_1 C$ 与平面 $D E F$ 的夹角的余弦值最大.
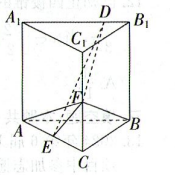
(1) 证明: $B F \perp D E$;
(2) 当 $m$ 为何值时, 平面 $B B_1 C_1 C$ 与平面 $D E F$ 的夹角的余弦值最大.
