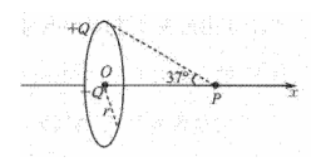
如图所示, 真空中电荷均匀分布的带正电圆环, 半径为 $r$, 带电量为 $+Q$, 圆心 $O$ 处固定一带电量为 $-Q$ 的点电荷, 以 $O$ 为坐标原点建立垂直圆环平面的 $x$ 轴, $P$ 是 $x$ 正半轴上的一点, 圆环上各点与 $P$ 点的连线与 $x$ 轴的夹角为 $37^{\circ}$, 静电力常量为 $k, \sin 37^{\circ}=0.6 、 \cos 37^{\circ}=0.8$, 下列说法正确的是

A. 圆环上所有的电荷在 $O$ 点产生的合电场强度大小为 $\frac{k Q}{r^2}$
B. 圆心 $O$ 处的 $-Q$ 在 $P$ 点产生的电场强度大小为 $\frac{9 k Q}{16 r^2}$
C. 圆环上所有的电荷在 $P$ 点处产生的电场强度大小为 $\frac{9 k Q}{25 r^2}$
D. $P$ 点电场强度的方向沿 $x$ 轴的负方向