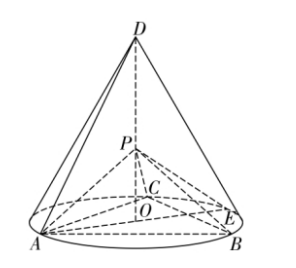
如图, $D$ 为圆锥的顶点, $O$ 是圆锥底面的圆心, $A E$ 为底面直径, $A E=A D$. $\square A B C$ 是底面的内接正三角形, $P$ 为 $D O$ 上一点, $P O=\frac{\sqrt{6}}{6} D O$.
(1) 证明: $P A \perp$ 平面 $P B C$;
(2) 求二面角 $B-P C-E$ 的余弦值.

(1) 证明: $P A \perp$ 平面 $P B C$;
(2) 求二面角 $B-P C-E$ 的余弦值.