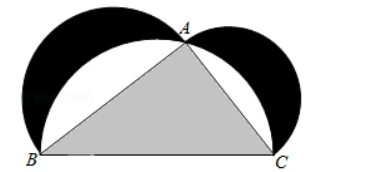
如图来自古希腊数学家希波克拉底所研究的几何图形. 此图由三个 半圆构成, 三个半圆的直径分别为直角三角形 $A B C$ 的斜边 $B C$, 直角边 $A B, A C$ - $\triangle \mathrm{ABC}$ 的三边所围成的区域记为 I, 黑色部分记为 II, 其余部分记为吕. 在 整个图形中随机取一点, 此点取自 $\mathrm{I}, \mathrm{II}$, III的概率分别记为 $\mathrm{p}_{1}, \mathrm{p}_{2}, \mathrm{p}_{3}$, 则 ( )
A
$\mathrm{p}_{1}=\mathrm{p}_{2}$
B
$\mathrm{p}_{1}=\mathrm{p}_{3}$
C
$\mathrm{p}_{2}=\mathrm{p}_{3}$
D
$\mathrm{p}_{1}=\mathrm{p}_{2}+\mathrm{p}_{3}$
E
F