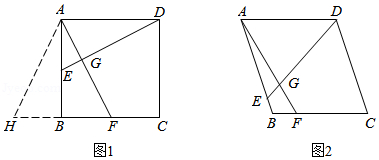
问题解决: 如图 1, 在矩形 $A B C D$ 中, 点 $E, F$ 分别在 $A B, B C$ 边上, $D E=A F, D E \perp A F$ 于点 $G$.
(1) 求证: 四边形 $A B C D$ 是正方形;
(2) 延长 $C B$ 到点 $H$, 使得 $B H=A E$, 判断 $\triangle A H F$ 的形状, 并说明理由.
类比迁移: 如图 2, 在菱形 $A B C D$ 中, 点 $E, F$ 分别在 $A B, B C$ 边上, $D E$ 与 $A F$ 相交于点 $G, D E=A F, \angle A E D=60^{\circ}, A E=6, B F=2$, 求 $D E$ 的长.