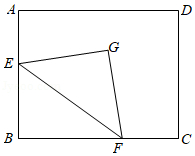
如图, 在矩形 $A B C D$ 中, $A B=4, A D=5$, 点 $E, F$ 分别是边 $A B$, $B C$ 上的动点, 点 $E$ 不与 $A, B$ 重合, 且 $E F=A B, G$ 是五边形 $A E F C D$ 内满足 $G E=G F$ 且 $\angle E G F=90^{\circ}$ 的点. 现给出以下结论:
(1) $\angle G E B$ 与 $\angle G F B$ 一定互补;
(2)点 $G$ 到边 $A B, B C$ 的距离一定相等;
(3)点 $G$ 到边 $A D, D C$ 的距离可能相等;
(4) 点 $G$ 到边 $A B$ 的距离的最大值为 $2 \sqrt{2}$.
其中正确的是 （　　）