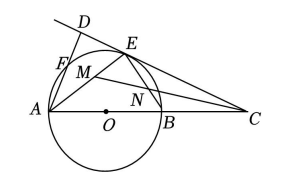
如图, 以 $A B$ 为直径的 $\odot O$ 上有两点 $E 、 F, \widehat{\mathrm{BE}}=\widehat{\mathrm{EF}}$, 过点 $E$ 作直线 $C D \perp A F$ 交 $A F$ 的延长线于点 $D$, 交 $A B$ 的延长线于点 $C$, 过 $C$ 作 $C M$ 平分 $\angle A C D$ 交 $A E$ 于点 $M$, 交 $B E$ 于点 $N$.
(1) 求证: $C D$ 是 $\odot O$ 的切线;
(2) 求证: $E M=E N$;
(3) 如果 $N$ 是 $C M$ 的中点, 且 $A B=9 \sqrt{5}$, 求 $E N$ 的长.