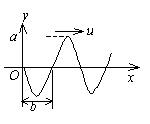
一平面简谐波以速度 $u$ 沿 $x$ 轴正方向传播,在 $t=t^{\prime}$ 时波形曲线如图所示. 则坐标原点 $O$ 的振动方程为
A
$y=a \cos \left[\frac{u}{b}\left(t-t^{\prime}\right)+\frac{\pi}{2}\right]$
B
$y=a \cos \left[2 \pi \frac{u}{b}\left(t-t^{\top}\right)-\frac{\pi}{2}\right]$
C
$y=a \cos \left[\pi \frac{u}{b}\left(t+t^{\prime}\right)+\frac{\pi}{2}\right]$
D
$y=a \cos \left[\pi \frac{u}{b}\left(t-t^{\prime}\right)-\frac{\pi}{2}\right]$
E
F