科数网
题号:6695    题型:多选题    来源:2023年普通高等学校招生全国统一考试《物理》全国甲卷A模拟试卷
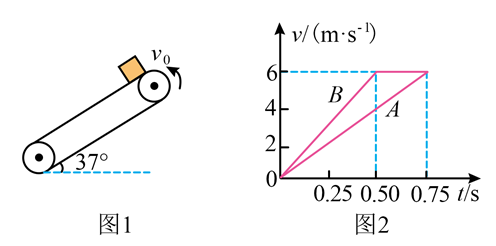
如图 1 所示, 一倾角为 37∘ 的传送带以恒定的速率 v0 逆时针转动。将两个不同的物块 A 、 B 轻轻并排放在传送带上, 二者并不接触 (图中只显示一个物块)。以平行于传送带向下的 方向为正方向, 两物块的速度一时间图像如图 2 所示。不计空气阻力, 重力加速度 g 取 10 m/s2, sin⁡37∘=0.6,cos⁡37∘=0.8 。关于两物块在传送带上的运动, 下列说法正确的是
A. 传送带的速度 v0 的大小为 6 m/s B. 传送带与物块 B 间的动摩擦因数为 0.75 C. 在 0:0.75 s 内, 两物块与传送带间产生的热量相等 D. 0.75 s 后, 若物块 A 在传送带上运动的时间少于 3 s, 则 A、 B 间的最大距离就不会变
答案与解析：
答案仅限会员可见 微信内自动登录 或 手机登录 或 微信扫码注册登录 点击我要 开通VIP