截面为等腰直角三角形的三棱镜如图甲所示。DE为嵌在三棱镜内部紧贴BB'C'C面的线状单色可见光光源，DE与三棱镜的ABC面垂直，D位于线段BC的中点。图乙为图甲中ABC面的正视图。三棱镜对该单色光的折射率为2，只考虑由DE直接射向侧面AA'CC的光线。下列说法正确的是
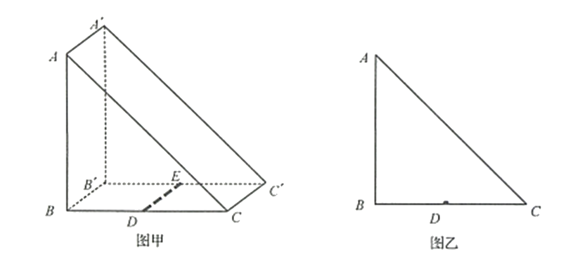
$ \text{A.}$ 光从 $A A^{\prime} C^{\prime} C$ 面出射的区域占该侧面总面积的 $\frac{1}{2}$
$ \text{B.}$ 光从 $A A^{\prime} C^{\prime} C$ 面出射的区域占该侧面总面积的 $\frac{2}{3}$
$ \text{C.}$ 若 $D E$ 发出的单色光频率变小, $A A^{\prime} C^{\prime} C$ 面有光出射的区域面积将增大
$ \text{D.}$ 若 $D E$ 发出的单色光频率变小, $A A^{\prime} C^{\prime} C$ 面有光出射的区域面积将减小